Das Wort „Subtrahieren“ kommt ebenso wie „Addieren“ aus der lateinischen Sprache und bedeutet „etwas entfernen“ oder „wegziehen“. Wenn man zwei Zahlen subtrahiert, zieht man von der ersten Zahl die zweite ab: Das Ergebnis ist im Zahlenraum der Natürlichen Zahlen somit immer kleiner. Die Subtraktion ist die Gegenoperation zur Addition. Zusammen mit Multiplikation und Division gehören die beiden Rechenoperationen zu den vier Grundrechenarten. In der Umgangssprache spricht man auch vom Minusrechnen. Seit dem Ende des 15. Jahrhunderts ist das Minuszeichen (-) das Rechenzeichen bei einer Subtraktion. 
9 – 4 = 5 bedeutet also nichts anderes, als dass die zweite Zahl von der ersten Zahl abgezogen wird.

Ein Hilfsmittel sowohl für Subtraktion als auch Addition ist der sogenannte Zahlenstrahl. Auf ihm lassen sich Subtraktionen sichtbar darstellen, sodass Kinder schnell und leicht begreifen, was Subtrahieren bedeutet. Wenn der Zahlenraum bekannt und verinnerlicht ist, können die ersten Subtraktionen erfolgen. Nehmen wir der Einfachheit halber an, dass die Kinder bis 20 zählen können und daher wissen, in welcher Reihenfolge die Zahlen kommen. Die Aufgabe lautet nun wie oben erwähnt: Subtrahiere 4 von 9, mathematisch ausgedrückt durch 9 – 4.

Auf dem Zahlenstrahl sucht man nun die erste Zahl, den sogenannten Minuenden. Von dort wird nach links weitergezählt, und zwar um den Betrag des sogenannten Subtrahenden. Das Kind zählt also von 9 ausgehend 4 Schritte nach links und landet bei der 5, dem Ergebnis. Je vertrauter die Kinder mit dem Zahlenraum und der Visualisierung durch den Zahlenstrahl sind, desto leichter wird es, die Rechnung auch ohne Zahlenstrahl oder sogar im Kopf durchzuführen.

Im Zusammenhang mit der Subtraktion ist wichtig zu wissen, dass – anders als bei der Addition – das Kommutativgesetz nicht gilt: Es spielt bei der Subtraktion eine wesentliche Rolle, was wovon abgezogen wird. 9 – 4 ist deshalb etwas völlig anderes als 4 – 9. Man vergleiche dazu die Addition mit ihrem Kommutativgesetz, nach dem gilt: 9 + 4 = 4 + 9.

Bei der Subtraktion gibt es – wie bei der Addition – einige Fachbegriffe, die man kennen muss, um sicher zu rechnen. Betrachten wir dazu unsere einfache Rechnung von vorhin:

9 – 4 = 5

9 ist der sogenannte Minuend (lat. „der zu Verringernde“), also die Zahl, von der abgezogen wird. 5 ist der Subtrahend (lat. „der Abzuziehende“), also die Zahl, die vom Minuenden abgezogen wird. Das Ergebnis wiederum ist der Wert der Differenz. Die ausgesprochene Rechnung aus unserem Beispiel lautet deshalb „Minuend minus Subtrahend ist gleich dem Wert der Differenz“, in unseren Zahlen „9 minus 4 ist gleich 5“.

Der Zahlenstrahl ist bei Addition und Subtraktion nützlich, hat aber bei größeren Zahlen Grenzen. Schneller geht es mit der schriftlichen Subtraktion, die beim Rechnen in der Grundschule eine wichtige Rolle spielt. Da es beim Subtrahieren verschiedene Methoden gibt, konzentrieren wir uns mit der Subtraktion mit Ergänzungsverfahren auf die wichtigste, die für Grundschülerinnen und Grundschüler relevant ist.

Bei der schriftlichen Subtraktion lassen sich auch große Zahlen auf einfache Art und Weise voneinander abziehen. Minuend und Subtrahend stehen dabei untereinander.

Beispiel 1: 289 – 117 = ?

Wir stellen zunächst Minuend und Subtrahend untereinander:

   289
- 117

Als nächstes subtrahieren wir in Einzelschritten die verschiedenen Stellen:

2 – 1 = 1
8 – 1 = 7
9 – 7 = 2

Die drei Einzelergebnisse hintereinander notiert ergeben den Wert der Differenz, in diesem Fall 172. Was aber, wenn eine Stelle des Subtrahenden größer ist als die des Minuenden? In diesem Fall arbeitet man mit dem Übertrag.

Beispiel 2: 222 – 117 = ?

Untereinander stellt man fest, dass eine Subtraktion eine negative Zahl ergeben würde, die in der Grundschule noch nicht eingeführt ist. Deshalb erhöht man die entsprechende Stelle des Minuenden um 10 und vermerkt das unter der nächstgrößeren Stelle mit einer 1:

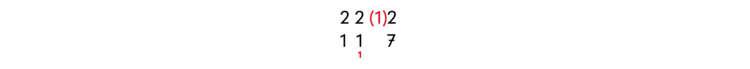
Anschließend kann man bequem die einzelnen Stellen subtrahieren:

2 – 1 = 1
2 – 1  – 1 = 0
12 – 7 = 5

Die drei Einzelergebnisse ergeben hintereinander geschrieben den Wert der Differenz: 105.

In einigen Bundesländern wird mit dem sogenannten Entbündelungsverfahren subtrahiert, welches für Kinder etwas schwieriger ist. Lehrwerke und Übungshefte von Cornelsen unterstützen Schülerinnen und Schüler beim Erlernen der schriftlichen Subtraktion.

Bruchrechnen gehört zu den fortgeschrittenen Rechenarten und wird in der Regel erst gegen Ende der Grundschulzeit behandelt, da hierfür auch die Multiplikation und die Division erforderlich sind. Folgende Regeln sind jedoch nützlich, um eine kurze Anleitung zum Bruchrechnen zu geben:

• Brüche bezeichnen immer Teile des Ganzen und werden durch zwei Zahlen ausgedrückt, die ober- und unterhalb des Bruchstrichs stehen.
• Im Nenner (unterhalb des Bruchstrichs) liest man, aus wie vielen Teilen ein Ganzes besteht. Im Zähler (oberhalb des Bruchstrichs) steht, wie viele Teile des Ganzen der Bruch enthält. Ein Beispiel: Der Bruch lautet 5/8. Das Ganze besteht also aus 8 Teilen, von denen der Bruch 5 enthält.
• Gut vorstellbar wird das anhand einer Torte aus gleichgroßen Stücken. Kauft jemand 5/8 der Torte, bekommt er oder sie 5 Stücke von 8.
• Brüche können nur subtrahiert (und addiert) werden, wenn die Nenner gleich sind. Ansonsten müssen die Brüche erweitert bzw. gekürzt werden. Sobald die Nenner gleich sind, muss man nur die Zähler subtrahieren. Ein Beispiel: 

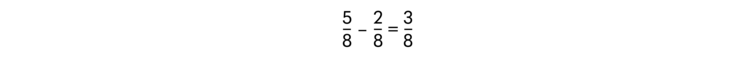
• Bruchrechnen wird in der Grundschule begonnen, die Vertiefung mit komplexeren Aufgaben findet aber erst ab der 5. Klasse statt.

Das Subtrahieren in der Grundschule beginnt ab der 1. Klasse, das schriftliche Subtrahieren mit großen Zahlen folgt meist ab der 3. Klasse. Zunächst wird der Zahlenraum bis 10/20 behandelt, den die Lehrkräfte dann schrittweise erweitern. Während viele Kinder vor der Einschulung bereits gut Zahlen oder Dinge voneinander abziehen können, geht es hier ums Rechnen mit den Zahlen.

Als Eltern können Sie mit Ihren Kindern immer wieder üben, wie man Zahlen subtrahiert. Folgende Tipps sind dafür hilfreich:

• Legen Sie Karten mit Aufgaben zur Subtraktion an und lassen Sie Ihr Kind regelmäßig damit rechnen. Die Lösung steht auf der Rückseite, sodass das Rechnen auch allein möglich ist.
• Kopfrechnen ist eine der besten Übungen. Stellen Sie Ihrem Kind über den Tag und die Woche verteilt immer wieder kleine Aufgaben, die ohne Zettel und Stift gelöst werden sollen.
• Lassen Sie Ihr Kind mit dem Taschengeld rechnen. Wenn es die Ausgaben vom eigenen Geld in der Geldbörse oder vom Sparkonto abzieht, muss automatisch subtrahiert werden.
• Geburtstage, Ferien und Uhrzeiten eignen sich gut, um die Subtraktion zu üben. Wie viele Tagen sind es noch bis zur Geburtstagsparty? Wie viele Tage muss man noch in die Schule gehen, bis die nächsten Ferien da sind? Wie viele Stunden und Minuten sind es bis zum Abendessen?

Übungshefte und Lehrwerke von Cornelsen helfen Ihnen ebenfalls dabei, Ihr Kind zum Meisterrechner zu machen. Die im Alltag bewährten und spannend gestalteten Aufgaben machen Spaß und sorgen dafür, dass Kinder sicher und stressfrei subtrahieren lernen.