{Klexer} Mit Kunst leichter Mathematik lernen
Spielerisch in die Geometrie einsteigen und Zahlvorstellungen fördern
Kinder sind allgemein gerne künstlerisch tätig und gestalten ihre eigenen Fantasiewelten. Mit Mitteln der Mathematik gelingt ihnen dies genauso gut wie einigen weltberühmten Künstler/-innen. Und ganz nebenbei erlernen sie wichtige Grundlagen der Grundschulmathematik.

Als Lisa einige Kreise mit dem Zirkel zeichnen sollte, war sie zunächst nicht begeistert. Sie kannte die feinmotorischen Herausforderungen beim Umgang mit den Zeichengeräten und wusste, dass ihre Kreise oft sehr wackelig wirken. So ergeht es vielen Grundschulkindern: Die noch zu gering entwickelte Feinmotorik, kleine Orientierungsschwierigkeiten, geringe Anstrengungsbereitschaft und das ungenügende Durchhaltevermögen verhindern manchmal den erfolgreichen Einstieg in die Geometrie. Mit geeigneten künstlerischen Ansätzen lässt sich die Begeisterung für geometrische Inhalte sehr gut unterstützen.
Schon die Wahl der Werkzeuge und Materialien ist entscheidend für den Erfolg: Ein weicher Bleistift (mindestens 2B), ein einfacher Zirkel ohne Stellschrauben (für Kinderhände besser handhabbar) und ein Lineal mit einer gut erkennbaren Maßeinteilung sind unverzichtbar. Dazu kommen diverse Kreisschablonen, ein Band oder Draht (als Zirkelersatz), Farb- oder Buntstifte sowie dickes Papier (ab 100g/m² und gerne in DIN A3).
Wo kommen denn die Kreise her?
Künstler/-innen und Mathematiker/-innen entdecken viele Ideen und Zusammenhänge durch Beobachtungen in der Natur.
Wir beobachten im Unterricht einen Wassertropfen, der auf eine Wasseroberfläche trifft. „Da entstehen ja ganz viele Kreise!“ Es entstehen sogar perfekte Kreise, welche sich durchdringen können. Die Kinder entdecken die bekannte geometrische Form neu und es wird ein Kreativspiel daraus.
Je zwei Kinder erarbeiten ein gemeinsames Bild aus Kreisen. Zuerst setzen beide Kinder abwechselnd und mit geschlossenen Augen eine vorgegebene Anzahl von Punkten auf das leere Blatt. Das sind die Tropfen, die auf das Wasser treffen. Freihändig zeichnen sie um jeden Punkt zwei beliebig große Kreise und leiten dabei die Eigenschaften eines perfekten Kreises ab: Die Kreislinie muss immer den gleichen Abstand zum Mittelpunkt haben. Das ist nicht einfach zu zeichnen, denn die Kreise überschneiden sich.
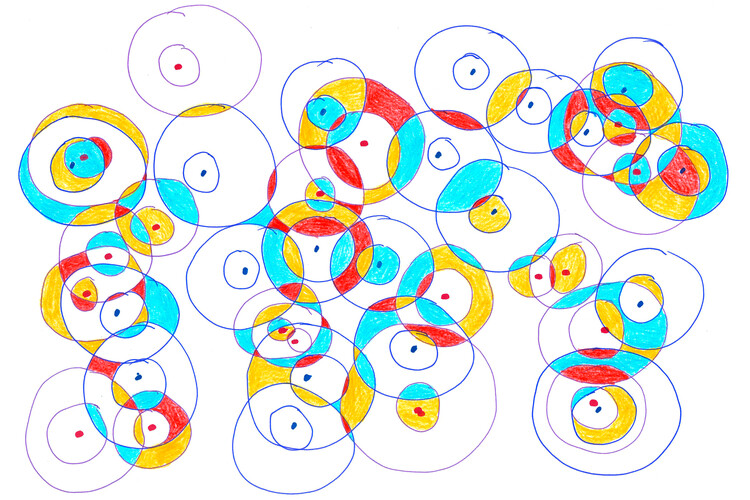
Für perfekte Kreise braucht man entweder sehr viel Übung oder Hilfsmittel und Zeichengeräte wie Schablonen, Band oder Zirkel. Bei der Nutzung der Hilfsmittel trainieren wir intensiv die Feinmotorik. Anschließend geben wir den einzelnen Elementen einen Namen: Kreismittelpunkt, Radius und Kreislinie. Und für die Kreativität ist auch noch Platz, wenn die Kinder die entstehenden Flächen farbig gestalten. Diese kleinen Kunstwerke sollten unbedingt präsentiert werden. Die Beschreibung der Entstehung ist automatisch die Wiederholung und Festigung der verschiedenen Fachbegriffe.
Lisa musste sich ganz schön anstrengen, bis sie den Zirkel sogar mit einer Hand benutzen konnte. Aus den Kreisbildern wurden Zirkelbilder mit immer komplizierteren Mustern. Nun war sie nicht mehr zu bremsen: Jede Übungsstunde endete mit einer neuen Zirkelbildidee.
Muster aus Kreisen
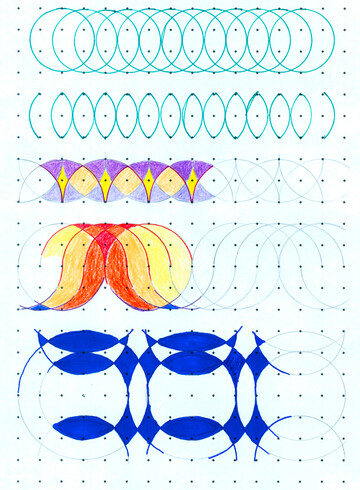
Was macht ein Muster aus? Formen und Farben wiederholen sich nach bestimmten Regeln. Berühmte Künstler wie Victor Vasarely oder Gerhard Richter haben solche komplizierten Regeln entwickelt und damit große Kunstwerke erschaffen. Und wie geht das bei einem Zirkelbild?
Zirkelbilder, Zirkelblumen oder Mandalas erfordern oft die sehr genaue Konstruktion von Schnittpunkten, welche zu neuen Kreismittelpunkten werden. Bei den ersten Übungen gelingt es nur wenigen Grundschulkindern diese exakt zu bilden. Daher stelle ich ein Arbeitsblatt mit einem Punkteraster zur Verfügung (siehe Kopiervorlage (KV) 1).
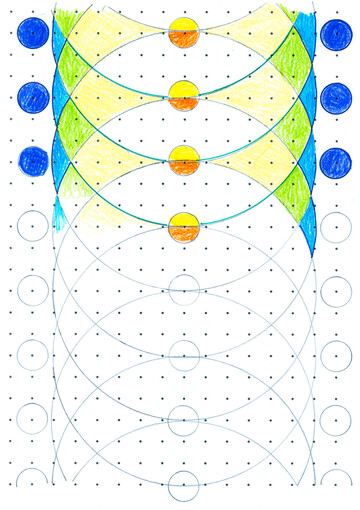
Hier können sich die Kinder auf die Handhabung des Zirkels konzentrieren und die Kreismittelpunkte nach einem gleichbleibenden Abzählmuster aus den Rasterpunkten auswählen. So entstehen verblüffende, schwierig wirkende Muster, die meine Schülerinnen und Schüler immer wieder überraschen.
Manch ein/-e kleinfacee/-r Mathekünstler/-in hat jedoch noch Schwierigkeiten, in einem vorgegebenen Raster Abzählmuster zu erkennen oder eine gleichbleibende, sich wiederholende Regel beliebig oft und fehlerfrei anzuwenden. Hierfür nutze ich ein weiteres Kreativspiel, bei dem gleichzeitig noch die Zahlvorstellungen vertieft werden.
Der Teppich aus Zahlbildern

Diese Übung lässt sich auch ohne aufwendige Vorbereitungen schnell und jederzeit realisieren. Ein einfaches kariertes Blatt, für kleinteilige Zahlenteppiche oder – zum Einstieg – ein Arbeitsblatt mit Ein-Zentimeter-Kästchen (siehe KV 2), in dem bei noch ungenügend entwickelter Feinmotorik leichter ausgemalt werden kann, reichen aus.

Für einen Zahlenteppich verwenden die Kinder ein Zahlbild aus dem Zahlenraum bis 10. Diese Zahlbilder sind bei mir unverzichtbare Bestandteile der Entwicklung von Zahlvorstellungen und grundlegender Rechenfertigkeiten. Mit einem dieser Zahlbilder wird die Fläche in regelmäßiger Anordnung gefüllt. Es entsteht ein Mosaikteppich bei dem hohe Konzentration und Ausdauer gefordert sind, denn kleine Abweichungen sind gut sichtbar. Die Korrektur solcher Abweichungen ist dann wiederum eine Ergänzung nach einer neuen einheitlichen Regel.
Durch die ständige Wiederholung der Zahlbilder prägen sie sich stärker ein und sind in anderen Anwendungen schneller notiert. Deshalb sollten auch die Ergebnisse dieser Kreativübung präsentiert und besprochen werden. Gerade bei der Präsentation werden die Kinder intensiver über ihre eigene Handlung reflektieren – und anschließend gerne noch weitere Teppichideen entwickeln.
Kreativität und Selbstständigkeit
Die beschriebenen Übungen haben den Vorteil, dass sie der Kreativität der Kinder freien Raum geben und gleichzeitig Fähigkeiten und Fertigkeiten für den Mathematikunterricht unterstützen. Die Bearbeitung kann sogar zur Förderung der Selbstständigkeit genutzt werden. Nach ersten Übungen unter Anleitung können die Schüler/-innen solche Arbeiten in einer Vertretungs-, Betreuungs- oder Freistunde ohne die Einflussnahme der Lehrkraft gestalten. Die Präsentation in einer kleinen Galerie im Klassenraum oder Schulflur ist oft eine besondere Motivation für die Kinder, die sich noch nicht so gerne mit Inhalten der Mathematik auseinandersetzen.
Buchtipps
Zum Autor
Frank Moede ist Diplomlehrer für Mathematik und Kunsterziehung und ausgebildeter Lerntherapeut für Rechenschwäche. Er arbeitet als Lerntherapeut in Magdeburg, unterrichtet als Dozent an einer Ausbildungsakademie Erzieher in Didaktik und Methodik und ist seit über zehn Jahren als Referent für den Cornelsen Verlag tätig.
